What Is Signal-to-Noise Ratio and Why Does It Matter?

By Amily Smith Last updated Jul 19, 2024

As technology enthusiasts, we often find ourselves immersed in the world of audio, electronics, and communication systems. One crucial aspect that significantly impacts the quality of these systems is the Signal-to-Noise Ratio (SNR). Whether you are an audio enthusiast, an engineer, or a designer, understanding SNR and its calculation is essential for achieving superior performance in your designs. In this comprehensive guide, we will explore what SNR is, its importance, and step-by-step methods to calculate it accurately.

What is Signal-to-Noise Ratio (SNR)?

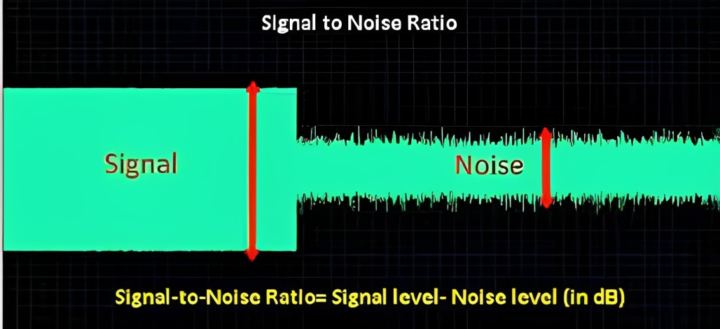
The signal-to-noise ratio (SNR) is a critical measuring metric used in science and engineering. It is the ratio of the power of the intended signal to the strength of the background noise. SNR is generally represented in decibels (dB) and is a key indication of signal clarity in the presence of noise interference.

Consider yourself chatting with one person in a busy, large space. Many people are having conversations at the same time, and some have vocal patterns that are similar to yours and your companion’s. This situation shows how difficult it is to distinguish each person’s speech.

A higher SNR, measured above 0 dB or greater than 1:1, indicates that the desired signal outnumbers the disruptive noise, improving communication and data transmission processes in a variety of applications.

The Importance of Signal-to-Noise Ratio

Signal-to-Noise Ratio (SNR) is important in many fields and applications for the following reasons:

Quality Assessment: SNR is a fundamental signal quality measure. A greater SNR indicates that the signal is stronger and clearer in comparison to the noise, resulting in superior audio, image, or video quality. A higher SNR in communication systems corresponds to improved voice or data clarity.
Reliable Communication: A high SNR ensures reliable data transfer in communication systems. It helps to eliminate errors and guarantees that transmitted information is received correctly, reducing the possibility of data loss or corruption.
Data Accuracy: A higher SNR is required in digital systems for precise signal processing and data analysis. Low SNR levels can cause data distortion or misinterpretation, leading to incorrect results.
Performance Optimization: A higher SNR is desirable in electronic systems to maximize performance. A high SNR, for example, in audio amplifiers ensures that the amplified sound is accurate to the original input.
Sensitivity and Detection: A high SNR is crucial in scientific instruments such as telescopes, radars, and sensors for detecting weak signals or dim objects. It increases sensitivity and allows researchers to discover and analyze signals that are remote or low in intensity.
Noise Reduction: Understanding the SNR enables engineers and researchers to identify noise sources and implement appropriate noise reduction or elimination strategies. This is critical in applications such as audio recording, where noise reduction techniques can greatly improve recording quality.
Radio Frequency and Wireless Communication: A greater SNR enables for more robust and reliable signal reception in wireless communication systems, especially in tough situations with interference or fading.
Network Performance: A higher SNR is required in data communication networks to achieve larger data rates and optimize network performance.
Diagnostic Imaging: In medical imaging, a high SNR is critical for producing clear and accurate images. It helps physicians to detect and diagnose medical conditions more effectively.
Energy Efficiency: A higher SNR can also help with energy efficiency in a variety of systems. In wireless communication, for example, a high SNR allows devices to transfer data at lower power levels while maintaining reliable communication, so conserving energy.

The Basics of SNR Calculations

The signal-to-noise ratio (SNR) represents the difference between the desired signal and the noise floor in its most basic form. Background transmissions from other devices or accidental interference generated on the same frequency comprise the noise floor. To compute the SNR, subtract the noise value from the signal strength value to measure the difference between the desired signal strength and the unwanted noise.

Consider a hypothetical scenario: your device’s radio receives a signal at -65 dBm while the noise floor is at -80 dBm. The resulting SNR would be 15 dB, suggesting a wireless signal intensity of 15 dB. Experts recommend an SNR of at least 20 dB for flawless connectivity in wireless networks to ensure smooth online browsing.

Let’s explore the SNR requirements versus SNR values:

SNR of 5 dB to 10 dB: Because the noise level closely approaches the desired signal, it falls below the minimum threshold for establishing a connection.
SNR of 10 dB to 15 dB: The accepted minimum for establishing an unreliable connection.
SNR of 15 dB to 25 dB: Typically considered the minimally acceptable level, providing poor connectivity.
SNR of 25 dB to 40 dB: Deemed to be good, ensuring decent connectivity.
SNR of 41 dB or higher: Considered excellent, offering robust connectivity.

SNR is frequently used to quantify the clarity and strength of electrical signals, although its application is far broader. It can be used to define ice core isotope levels, biological signaling between cells, or even the audio sound quality of car amplifiers and source units (DVD, CD, or Digital). With audio components, however, the SNR is always expressed as a positive value. An SNR of 95 dB, for example, indicates that the audio signal level is 95 dB greater than the noise level, making it preferable to an SNR of 80 dB.

How to Calculate Signal to Noise Ratio

Measure the Signal Power (P_signal)
- For audio signals: Using appropriate equipment or software, determine the power of the desired audio signal (e.g., in watts or volts).
- For images: Measure the average pixel intensity of the signal region of interest. To calculate the signal power, square the intensity values and average them.
- For electronics: Measure the power of the signal at the output of the system or device.
Measure the Noise Power (P_noise)
- For audio signals: Measure the power of the background noise or unwanted interference in the same units as the signal power.
- For images: Measure the average pixel intensity of the noise region. Square the intensity values and average them to get the noise power.
- For electronics: Measure the power of the noise at the output of the system or device.
Calculate SNR in dB
- Use the formula: SNR (dB) = 10 * log10(P_signal / P_noise)

Now, let’s go through a practical example of calculating SNR for an audio recording:

Example: Suppose you have recorded a guitar performance, and you want to determine the SNR of the recording to assess its audio quality.

Step 1: Measure the Signal Power (P_signal):

Play the audio recording and measure the average power of the guitar signal. You can use software or an audio power meter to do this.
Assume the guitar signal has an average power of 50 watts (W).

Step 2: Measure the Noise Power (P_noise):

Pause the audio recording during a silent part where there is no guitar playing or any other desired signal. This portion will contain only background noise.
Measure the average power of the background noise using the same method as in Step 1.
Let’s say the average power of the background noise is 2 watts (W).

Step 3: Calculate SNR in dB:

Use the formula: SNR (dB) = 10 * log10(P_signal / P_noise)

SNR (dB) = 10 * log10(50 / 2) ≈ 10 * log10(25) ≈ 10 * 1.397 ≈ 13.97 dB

In this example, the SNR of the guitar recording is approximately 13.97 dB. This indicates that the guitar signal is around 13.97 decibels stronger than the background noise present in the recording.

A higher SNR value signifies better audio quality, as it suggests a stronger and more prominent guitar signal relative to the background noise. In contrast, a lower SNR value would imply a noisier recording with potentially reduced clarity and fidelity in the guitar performance.

Signal-to-Noise Ratio Formula and its Impact on Channel Capacity

Due to their reliance on radio signals, the signal-to-noise ratio (SNR) has a substantial impact on the operation of many wireless networks, including Bluetooth, Wi-Fi, 4G, 4G LTE, and 5G. Because these communication systems use radio signals, each has a maximum channel capacity that, curiously, increases with higher SNR.

The interaction of channel capacity, bandwidth, and SNR determines the maximum capacity of communication channels. Claude Shannon established this insightful correlation during World War II, and it is now commonly recognized as Shannon’s Law or the Shannon-Hartley theorem.

Shannon’s Law states that the channel capacity (expressed in bits per second) is dictated by the average received signal power (S), average noise power (N), and bandwidth (W) in Hertz. The formula for the theorem demonstrating this relationship is:

C = W log2(1 + S/N)

where:

C represents the channel capacity (bits/s)

S signifies the average received signal power

N denotes the average noise power

W stands for the bandwidth

Calculating the SNR precisely is crucial for producing efficient and accurate designs. Engineers and scientists in the domains of electronics and science rely on this computation to acquire significant insights into design functionality and performance. Identifying the feasibility of a design before the manufacturing phase is critical, and this needs careful study using calculations and simulations.

Accurate SNR calculations not only aid in successful design implementation, but also in maximizing communication channel capacities and assuring dependable transmission rates.

How to Improve Signal to Noise Ratio

Improving the Signal-to-Noise Ratio (SNR) is essential to enhance the quality, reliability, and performance of various systems and applications.

Here are some strategies to improve SNR:

Signal Filtering: Use signal filtering techniques to eliminate or reduce undesirable noise components. Depending on the application, filtering can be done with analog or digital filters.
Noise Reduction Techniques: Use noise reduction algorithms to reduce background noise while preserving the target signal. These techniques are frequently used in audio processing and speech recognition applications.
Higher Signal Power: If possible, boost the power of the desired signal. This can be accomplished in communication networks by raising transmitter power or employing more efficient signal modulation algorithms.
Bandwidth Optimization: Increase the signal bandwidth in communication networks. This enables a higher data rate as well as better resilience to noise and interference.
Improved Antennas and Receivers: Use better-quality antennas and receivers intended to reduce noise and interference.
Error Correction Codes: Implement error correction codes in data transmission systems to detect and rectify errors produced by noise during signal transmission.
Spatial Diversity: In wireless communication, use multiple antennas or spatial diversity techniques to improve SNR and reduce fading effects.
Thermal Noise Reduction: In electronics, lower the temperature of sensitive components to reduce thermal noise.
Shielding and Grounding: Properly shield sensitive electronic components and use effective grounding techniques to minimize electromagnetic interference.
Source Isolation: Physically isolate or position signal sources away from noise sources to minimize coupling.
Time Averaging: Average multiple measurements over time to reduce random noise contributions and improve SNR in the measured values.
Sensitivity Settings: Adjust the sensitivity settings of devices or systems to optimize SNR based on the specific requirements.
Use Low-Noise Components: Select components with low noise characteristics, such as low-noise amplifiers or low-noise sensors.
Signal Synchronization: In some cases, synchronization of signal transmission and reception can be used to improve SNR by reducing timing errors and jitter.

FAQ’s

What is Signal-to-Noise Ratio (SNR)?

Signal-to-Noise Ratio (SNR) is a crucial measuring metric used in science and engineering. It represents the ratio of the power of the intended signal to the strength of the background noise. SNR is usually expressed in decibels (dB) and is a key indicator of signal clarity in the presence of noise interference.

Why is Signal-to-Noise Ratio (SNR) important?

SNR is critical in various sectors and applications for a variety of reasons. It improves data accuracy, optimizes system performance, improves sensitivity and detection in scientific equipment, decreases noise, and has an impact on network performance, diagnostic imaging, and energy efficiency.

How can I calculate Signal-to-Noise Ratio (SNR)?

SNR is calculated by measuring the signal and noise power. Measure the power of the desired audio signal and background noise for audio signals. Measure pixel intensities in signal and noise sections of pictures. Measure the power at the output of an electronic device. Then apply the following formula: SNR (dB) = 10 * log10(P_signal / P_noise).

What is the significance of Signal-to-Noise Ratio (SNR) in wireless networks?

In wireless networks, SNR is critical in determining channel capacity and data transmission rates. Higher SNR levels result in bigger channel capacities and more reliable communication. It has a direct impact on the efficiency and performance of wireless communication networks.

How can I improve Signal-to-Noise Ratio (SNR)?

Signal filtering, noise reduction techniques, increasing signal power, optimizing bandwidth, using better antennas and receivers, implementing error correction codes, employing spatial diversity, reducing thermal noise, proper shielding and grounding, source isolation, time averaging, adjusting sensitivity settings, and using low-noise components are some strategies for improving SNR.

What is the relationship between Signal-to-Noise Ratio (SNR) and channel capacity?

The Shannon-Hartley theorem establishes the relationship between signal-to-noise ratio (SNR) and channel capacity. C = W * log2(1 + S/N), where W is the bandwidth, S is the average received signal power, and N is the average noise power, gives the channel capacity (C) in bits per second. Higher SNR levels in communication channels result in improved channel capacity and faster data transmission rates.

Conclusion

The Signal-to-Noise Ratio (SNR) is an important statistic that influences the quality and performance of audio, communication, and electronic systems. Understanding SNR and its computation is critical for designing for greater functionality and reliability. Higher SNR values result in clearer signals, improved data transmission, and better system performance. Engineers can increase signal clarity and maximize efficiency in a variety of applications by precisely assessing and enhancing SNR using various ways.