What Is a RSA Algorithm?

Millions of people use advanced technologies in their personal and professional lives every day, leading to regular storage and exchange of personal data. Without proper protection for their devices, users are at risk of fraud, which can cause major issues and increase cybercrime. Encryption and cybersecurity are crucial in fighting cyber threats. In this article, we will explore one of the key encryption algorithms: the RSA algorithm.

What is the RSA algorithm (Rivest-Shamir-Adleman)?

The RSA algorithm (Rivest-Shamir-Adleman) is a core component of a cryptosystem—a set of cryptographic algorithms designed for specific security functions—that supports public key encryption. It is commonly used to secure sensitive data, particularly during transmission over insecure networks like the internet.

First introduced in 1977 by Ron Rivest, Adi Shamir, and Leonard Adleman from the Massachusetts Institute of Technology, RSA’s principles were preceded by a public key algorithm created by British mathematician Clifford Cocks in 1973. However, Cocks’ work remained classified by the U.K.’s GCHQ until 1997.

Public key cryptography, also known as asymmetric cryptography, involves two distinct but mathematically connected keys: a public key that can be shared freely and a private key that must be kept secret.

In RSA cryptography, both the public and private keys can be used to encrypt a message. The key opposite to the one used for encryption is employed for decryption. This characteristic makes RSA a leading asymmetric algorithm, as it ensures the confidentiality, integrity, authenticity, and non-repudiation of electronic communications and data storage.

RSA is integral to many protocols, such as Secure Shell (SSH), OpenPGP, S/MIME, and SSL/TLS, for encryption and digital signatures. It is also widely used in software applications, including browsers, which require secure connections over the internet or need to validate digital signatures. RSA signature verification is a frequently performed task in networked systems.

Why is the RSA algorithm used?

RSA’s security is based on the challenge of factoring large integers that result from multiplying two large prime numbers. While multiplying these primes is simple, deducing the original primes from the product—known as factoring—is considered impractical with even the most advanced supercomputers due to the time required.

The most intricate part of RSA cryptography is generating the public and private keys. This involves producing two large prime numbers, p and q, using the Rabin-Miller primality test algorithm. The modulus, n, is then calculated by multiplying p and q. This modulus is shared by both the public and private keys and connects them. The size of this modulus, often expressed in bits, is known as the key length.

The public key comprises the modulus n and a public exponent, e, which is typically set to 65537. This prime number is chosen for its optimal size. As the public key is meant to be shared, the value of e does not need to be kept secret.

The private key includes the modulus n and the private exponent d, which is determined using the Extended Euclidean algorithm to find the multiplicative inverse with respect to the totient of n.

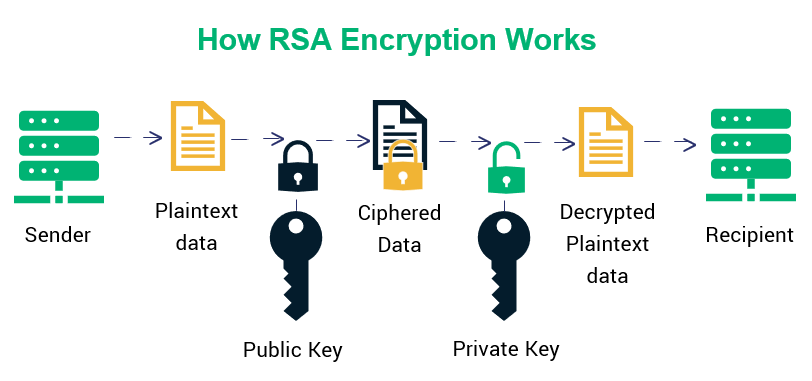
How does the RSA algorithm work?

The RSA algorithm involves four stages:

1. Key Generation: Create a private key (to keep) and a public key (to share).
2. Key Distribution: Distribute the public key across the network.
3. Encryption: The sender encrypts the message using the receiver’s public key.
4. Decryption: The receiver decrypts the message using their private key.

Alice generates her RSA keys by choosing two prime numbers: p=7 and q=17. She calculates the modulus as n=p×q=119 and the totient as ϕ(n)=(p−1)×(q−1)=96. Alice selects 5 as her RSA public key exponent e and determines her RSA private key d using the Extended Euclidean algorithm, which results in d=77.

Bob wants to send Alice an encrypted message M, so he obtains her RSA public key (n, e), which in this example is (119, 5). His plaintext message, represented by the number 12, is encrypted into ciphertext C as follows:

M^e mod n = 12⁵ mod 119 = 54 = C

When Alice receives Bob’s message, she decrypts it using her RSA private key (d, n) with the following calculation:

C^d mod n = 54⁷⁷ mod 119 = 12 = M

To digitally sign a message, Alice would first create a hash—a digest of her message to Bob—then encrypt this hash with her RSA private key and attach it to the message. Bob can verify the authenticity and integrity of the message by decrypting the hash with Alice’s public key. If the decrypted hash matches the hash of the original message, it confirms that the message was indeed sent by Alice and has not been altered.

Alice could also encrypt her message using Bob’s RSA public key to ensure confidentiality before sending it. Additionally, a digital certificate contains identifying information about the certificate’s owner and their public key. Certificates are signed by a certificate authority, simplifying the process of obtaining and verifying public keys.

How is RSA secure?

RSA security is based on the difficulty of factoring large integers. As computing power advances and more efficient factoring algorithms emerge, the capability to factor increasingly larger numbers also improves.

The strength of encryption is directly related to key size. Increasing the key length can significantly enhance security, though it may also affect performance. RSA keys are commonly 1024 or 2048 bits long, but experts now consider 1024-bit keys insufficiently secure against all threats. Consequently, government agencies and certain industries are shifting to a minimum key length of 2048 bits.

Unless there is an unexpected breakthrough in quantum computing, it will be some time before longer keys become necessary. Meanwhile, elliptic curve cryptography (ECC) is gaining traction as an alternative to RSA for public key cryptography. ECC offers faster, smaller, and more efficient cryptographic keys.

Modern hardware and software are ECC-compatible, and its adoption is likely to increase. ECC provides comparable security with less computational power and reduced battery usage, making it a better option for mobile applications compared to RSA.

Recently, a team of researchers, including Adi Shamir, a co-inventor of RSA, successfully created a 4096-bit RSA key using acoustic cryptanalysis. However, it’s important to remember that all encryption algorithms remain vulnerable to potential attacks.

FAQ’s

What is the RSA algorithm?

RSA is a public key encryption method used to secure data by encrypting and decrypting messages with a pair of keys: a public key and a private key.

Why is RSA secure?

RSA’s security relies on the difficulty of factoring large numbers into their prime factors. This challenge makes unauthorized decryption extremely difficult.

How are RSA keys generated?

RSA keys are generated by selecting two large primes, calculating their product (modulus), and then deriving the public and private keys using mathematical formulas.

How does key size affect RSA encryption?

Larger key sizes enhance security but can slow performance. RSA keys are typically 1024 or 2048 bits, with 2048 bits being more secure against current threats.

What is a digital signature in RSA?

A digital signature involves hashing a message and encrypting the hash with the sender’s private key. This verifies the sender’s identity and the message’s integrity.

Can RSA encrypt data and sign messages?

Yes, RSA can both encrypt data using the recipient’s public key and sign messages using the sender’s private key.

How does RSA compare to elliptic curve cryptography (ECC)?

ECC offers similar security with smaller key sizes and less computational power, making it more efficient for some applications compared to RSA.

Are there any vulnerabilities with RSA?

RSA is generally secure but can be compromised by advances in computing power and cryptographic methods. Staying updated with current standards is important.

What is a digital certificate?

A digital certificate verifies the identity of the certificate holder and includes their public key, simplifying the secure exchange of public keys.

Conclusion

The RSA algorithm remains a cornerstone of modern cryptography, providing robust security through its complex key generation and encryption processes. By relying on the difficulty of factoring large integers, RSA ensures that sensitive data can be securely transmitted and authenticated. While RSA is highly effective, advancements in technology and the rise of elliptic curve cryptography (ECC) suggest that ongoing developments in cryptographic techniques will continue to shape how we protect our digital communications. As we move forward, maintaining up-to-date practices and exploring new cryptographic methods will be essential for safeguarding against emerging threats.